In the last couple years the BC government has changed the radio frequencies used on all the forest service roads (FSRs). They used to post the frequencies used so that you could type them in to your handheld radio. With your radio programmed you are able to communicate with other users of the road, ie. logging trucks. The radio system is primarily there as a safety procedure to prevent collisions on BC’s narrow backroads. The cryptic system that they are now using takes away that safety tool if you are not prepared.
I was caught off guard in 2015 when the radio frequency was removed from the West Pavillion FSR which I use to access some of my claims. A sign that mentioned the change was in place but it did not state the new channel.
Here is the government site showing which channels are used on which roads: Resource road radio channel maps
This post will help you program your radios for BC’s new RR radio system. You will need a few things for this:
- A Radio
- Programming Cable
- A Computer
- Radio Software
I am using a Baofeng UV-5R programmable radio. I can’t say enough good things about this radio. It is inexpensive (~$30), powerful and has lots of memory channels. The coolest feature is that they are field programmable too. More on the Baofeng UV-5R here, Gear Review: Baofeng Handheld Radio. This guide works for other radios such as a Kenwood or Motorola, although you might need different software.
The cable that I’m using is a FTDI 2-pin Kenwood style. It works for Baofeng and Kenwood radios. For this post I’m using my laptop running Ubuntu linux. But this guide will work with Windows too.
The software is really the key to the whole programming procedure. There is an excellent open source program called CHIRP which stands for CHInese Radio Project. CHIRP was designed to make it easy to program cheap Chinese radios such as the Baofeng, it also works on just about any other radio out there and its free.
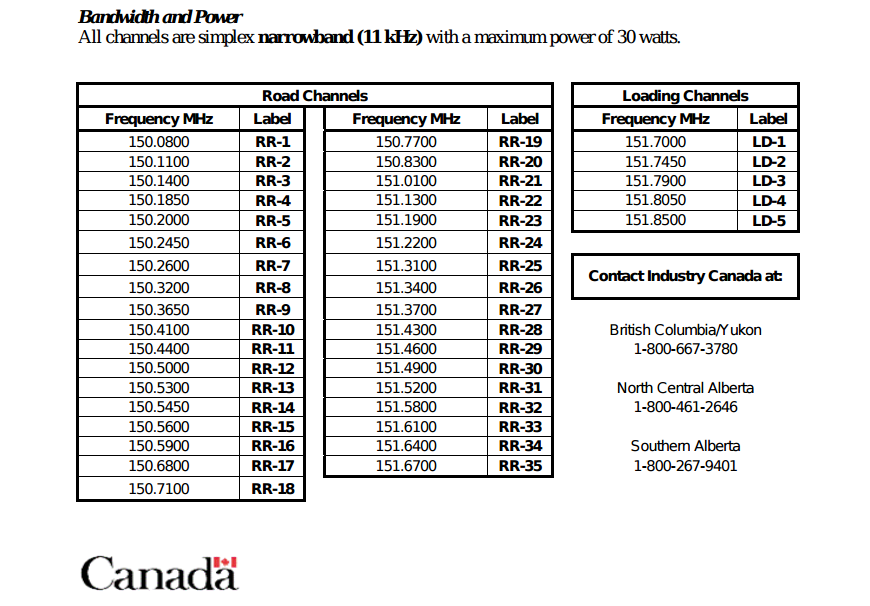
OK lets get started. The first thing that we have to do is get a list of frequencies. I found them on a government website, but I’ll save you the trouble and post them right here.
 You need to download and install CHIRP, on Ubuntu all you have do is run this command:
You need to download and install CHIRP, on Ubuntu all you have do is run this command:
sudo apt-get install chirp
That will download and install the latest version from Ubuntu’s repositories. If you are running Windows or Mac you can download CHIRP from their website here, CHIRP Site. Installation is easy, just run the .exe file and you’re good to go.
Next start up the program, on linux you need to run it as root (AKA administrator) you can do that with the following command:
sudo chirpw
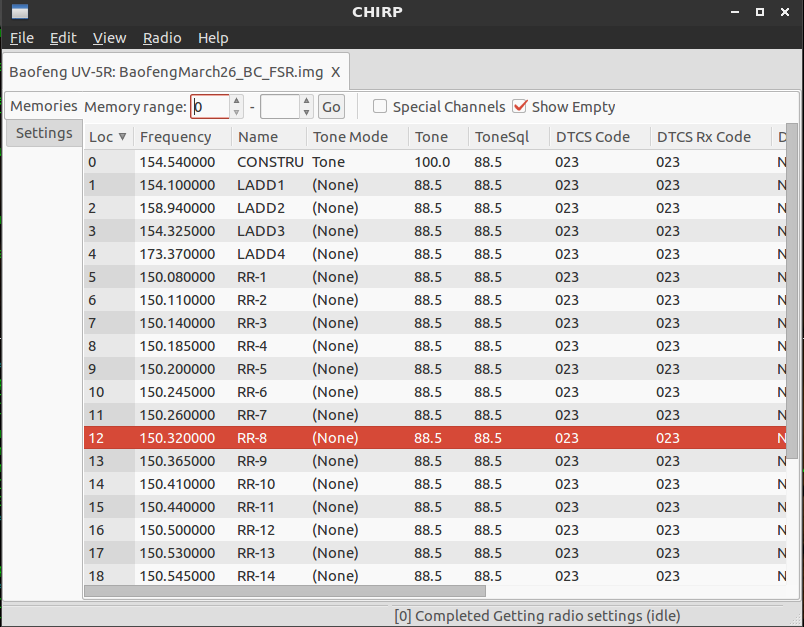
OK, now that CHIRP is started you have a few options. You can clone your radio’s existing channels and modify them. You can start a new file or load in an existing one. Lets start one from scratch. Click on the File menu and select “New”. In my example I added a couple extra channels at the top.
It’s a pretty straightforward application. The window functions a lot like a spreadsheet, there is a row for each channel and different parameters are defined in each column. The BC RR channels are pretty basic so you can ignore most of the columns. The RR channels are simplex, that means that they use the same frequency for transmit and receive. Most public channels are simplex. They have no carrier tone or any other funny business. So we just have to enter the frequencies and the name. Leave the rest of the settings at the default values.
After entering all 35 channels you are ready to load them onto the radio. To do that first connect the programming cable to the radio. It plugs into the port where you can add an external microphone. See photo below:
Make sure the radio is turned off when you connect the cable. Otherwise it could shock the memory and wreck the radio. The software will need to know which serial port you have connected to. In linux you can get that information with the following command:
dmesg | grep tty
Look for the line that looks like this:
[147117.481257] usb 2-3: FTDI USB Serial Device converter now attached to ttyUSB0
That is telling us that the programming cable is on port “ttyUSB0”. In Windows the easiest way is to look at your serial ports in the device manager.
Now you can upload the channels to the radio. Turn on the radio with the programming cable attached. Then choose “Upload to radio” from the Radio menu in CHIRP. You’ll be prompted for the serial port, in my case ttyUSB0. You will also need the radio make and model.
Once you hit OK, the upload will begin. You’ll get a nice progress bar to show you how its going.
That’s about it. Make sure that you turn off the radio before you disconnect the programming cable. Now you’re ready to hit the back roads and communicate with other travellers.
Update on Laws Regarding Programmable Radios 2021
There has been a lot of feedback about this post stating that Baofeng radios are illegal, you need a license, and things of that nature. We were recently contacted by a representative of Innovation, Science and Economic Development Canada (ISED, formerly Industry Canada) and we’ll share the factual information here.
First of all, it’s not illegal to program your own radio in Canada. ISED wants you to have a license for the channels that you are using though.
Most of the regulations in the Radiocommunication Act depend on two principles.
1) Radio spectrum is a limited resource
2) Prevention of “Harmful Interference”
ISED likes to state that the radio spectrum is a limited resource. What does that really mean? Well, there is a limit to the number of frequencies that can be used in a particular area without having overlapping signals. Spectrum management is important in congested areas to maintain quality for all users. This is one of the main goals of ISED. They regulate a lot of radio stuff beyond VHF frequencies on backroads, including cell towers, police and military communication, maritime communication, aviation, and other wireless transmissions. Managing wireless radio is important for our society to function properly. Calling it a “limited resource” is a little weird but management of the frequencies that are being used is important.
According to the ISED representative that contacted us the reason for most of the regulations is to prevent harmful interference. This is the definition that was provided by ISED:
“Radio interference is an adverse effect that could degrade, obstruct or interrupt the use or functioning of a radio. Radio interference can happen for a variety of reasons, and most of the time they are unintentional. In certain situations, the interference can be harmful.
Public safety agencies are critically dependant on their radio systems to provide services to the public. When their radio systems are interfered with, the ability to protect and serve the public is impaired, leaving human lives and property at risk. Non-public safety operations can be negatively impacted by degradation or repeated interruptions to radiocommunication systems. In some cases the interference may not be harmful, but it could still reduce the quality and usability of a radio system. When providing access to spectrum and regulating its use, ISED seeks to maximize the economic and social benefits that Canadians derive from the spectrum, and minimizing interference is a key part of this objective.”
The Radiocommunications Act defines harmful interference as follows:
harmful interference means an adverse effect of electromagnetic energy from any emission, radiation or induction that
- (a) endangers the use or functioning of a safety-related radiocommunication system, or
- (b) significantly degrades or obstructs, or repeatedly interrupts, the use or functioning of radio apparatus or radio-sensitive equipment;
OK, that’s some background on the laws. So what does that have to do with Baofeng radios and using them to communicate for safety reasons on BC’s backroads? The short answer is nothing.
If a radio is programmed correctly it won’t interfere with other radios and won’t cause “harmful interference”. A Baofeng radio is fully capable, and often much more capable, than a Kenwood, Icom or Motorolla that you can purchase from a certified radio shop. We’ll see some of the specific laws below.
Radio equipment in Canada requires licensing. There are two areas where a license is needed. The radio itself needs to be certified, this is usually done at the manufacturer level. Radios that aren’t certified by the manufacturer are required to have a license issued for its use. The criteria for obtaining such a licence is available here: RSS-119 – Land Mobile and Fixed Equipment Operating in the Frequency Range 27.41 – 960 MHz.
Baofeng radios cannot be licensed in Canada because they allow the user to program frequencies with external controls. That goes against Section 3.2 of the Radio Standards Specification
3.2 Transmitters With External Frequency Selection Controls
In order to prevent radio interference caused by end-user transmissions on unauthorized frequencies, transmitters with external frequency selection controls and/or frequency programming capability shall conform to the following:
- (a)Transmitters with external frequency selection controls shall operate only on authorized channels which have been preset by the manufacturer, equipment supplier, service technician or maintenance personnel.
- (b)Transmitters with frequency programming capability must have at least one of the following design characteristics, which prevent the user from altering the preset frequencies:
- Transmitters with external controls available to the user can only be internally modified to place the equipment in the programmable mode. Furthermore, while in the programmable mode, the equipment is not capable of transmitting. The procedure for making the modification and altering the frequency program is not available to the user of the equipment.
- Transmitters are programmed for frequencies through controls that are inaccessible to the user.
- Transmitters are programmed for frequencies through the use of external devices or specifically programmed modules that are available only to the service technician or maintenance personnel.
- Transmitters are programmed through cloning (i.e., copying a program directly from another transmitter) using devices and procedures that are available only to the service technician or maintenance personnel.
Since the Baofeng radios cannot be licensed use of these radios contravenes subsection 4(1) of the Radiocommunication Act which states:
4 (1) No person shall, except under and in accordance with a radio authorization, install, operate or possess radio apparatus, other than
- (a) radio apparatus exempted by or under regulations made under paragraph 6(1)(m); or
- (b) radio apparatus that is capable only of the reception of broadcasting and that is not a distribution undertaking.
According to ISED violation of Section 4(1) can carry a potential fine up to $250. Although that is really just academic since they don’t actually enforce that law.
According to ISED, for a radio using RR and LADD channels, a radio license is required. ISED will only issue a radio license for a radio that is certified and meets the certification requirements. A certified radio should display an IC number on its label (usually this is next to the FCC number). The conditions of use for RR and LADD channels are noted here: RR — British Columbia Resource Road Channels and B1 — Western and Northern Canada Mobile-Only Frequencies.
An ISED radio license costs $42.65/year per radio and is valid from April 1 to March 31 (the following year). This is a flat fee and not dependant on the number of channels.
Operating without a license can theoretically face fines if ISED finds out that you are doing so and has your contact information. You can see the potential fines under the Administrative Monetary Penalties (AMP).
According to the AMP penalties, operating without a license carries a potential fine of $1,000 for the first offense and up to $2,000 for the second offense.
Here’s the kicker though and this is really important, ISED depends on “voluntary compliance”. I asked the representative from ISED for evidence of fines that have been given out in the past and he confirmed that they don’t actually give out fines. They have no means to enforce these laws and do not check what radios people are using. There have been rumors on certain 4×4 groups that ISED sets up roadblocks on FSRs to catch people with illegal radios. Those rumors have been confirmed to be false by the ISED.
It seems odd that the FSR roads are open to the public but the Canadian government is limiting access to radio use by means of a licensing program. It’s also odd that they go out of their way to prevent users from using an inexpensive field-programmable radio. ISED’s explanation of “harmful interference” is ridiculous. In reality, you are protecting yourself and other road users by having communication available.
In summary, there are laws regarding field-programmable radios but they are not enforced. Similar to how there are laws regarding downloading movies or consuming fake maple syrup (actually, that law was repealed in 2019).
To get set up with a compliant radio in BC will typically cost about $1000 for something like a Kenwood NX1200 plus programming costs. Plus $43/year for the rest of your life. In contrast, you can get a BaoFeng UV-82HP for less than $100 CAD which is a better radio and no additional costs. The truck-mounted version is also a very good choice (BTECH Mini UV-25X4).
When driving on backroads in BC it is essential to have a radio. There are loaded logging trucks coming around tight corners and they will not know you’re there unless you have an appropriate radio and are calling out kilometers. A programmable radio such as a Baofeng will not cause interference of any kind and will allow you to communicate safely for a reasonable price. If you’re the kind of person who loses sleep because they downloaded a movie off a BitTorrent site then you should probably get an ISED radio license and a certified radio. For everyone else, there are great options out there and you can use this useful guide to program your own radio.
It should be noted that there are serious radio laws that are actually enforced. Such as transmitting on police or emergency bands. Don’t ever do that, as a joke or otherwise. It is perfectly legal to listen on those channels but very much illegal to transmit.
Also keep in mind that RR and LADD channels are for professional use and your own safety, not for chit-chat or talking to your buddies. There are thousands of channels and if you have a programmable radio you can set a special channel for you and your buddies while keeping the RR channel open for legitimate use.



This is great info!
I’m using Kenwood software for a radio I have and I was wondering how you find out what channels are “Narrow Band” or “Wideband” like the Ladd channels for instance?
Thank you in advance!
Thanks have been looking for the “RR” Frequencies
You might want to note that when you make a new channel file that it has to be saved as an .img file or the radio will not recognize it. For some reason my computer wanted to save it as a .csv and it would not work. Easiest way is to clone a download of what is in the radio already.
Thanks for the info.
Dale
Saved as a favorite, I really like your site!
Awesome post.
Does any one know anybody who programs baefeng radios on Vancouver Island ? I must have taken a stupid pill because I can not program this BF-F8HP . My computer doesn’t like the CHIRP program , won’t recognize the port . Damn radio talks to me in Chinese, I think I did that to it , not sure how .
Any ways , I need some help with it , I live In the Comox Valley .
IF you can’t do it on CHIRP, you can program on the radio directly. First set it to English then change the settings as required.
I”d help you but I’m in the Lower Mainland.
For use with a local transport company, I am trying to program the F8HP to channels with Tx, Rx, Tx Tone, Rx Tone (4 numbers) and can’t figure out how to do it with CHIRP. Is there a FAQ around or anyone on here I can talk to about it? Just not sure what all the mode choices mean…
I had this problem. 1st, the plug was not fully inserted into the radio. It’s a tight fit. Also, the program was reading from the wrong com port. Check Device Manager to see which one the radio is actually using. Mine uses 5. Hope that helps.
hey i was wondering if you could send me a copy of that programming?
The frequencies are posted here and there is a screenshot of the CHIRP layout. It’s pretty straightforward.
Hi I am totally new to this. Want to add the RR Channels to my radio. I have added the frequencies using CHIRP, but all of the other fields are empty. Do I need anything in those fields? Thanks in advance for any help.
Check the screenshot in the article. You do need info in the other fields. The only thing that will be different for each channel is the frequency and name.
More info here if you’re still confused: http://issaquahcitizencorps.org/Baofeng%20UV-5R%20CHIRP%20Programming%20Guide%20IWillPrepare.pdf
Thanks for the response. I noticed in the screenshot that the ‘Tone Mode” for the RR channels says ‘none’. If I leave it at ‘none’, I cannot change any of the other fields. If its is on “Tone” then I can change them to match. I am assuming I am missing something obvious. I will also check out the link. Thanks!
He stated that these BC RR and LD channels do not use tones, so you do not need to fill in the other fields. You only need to fill in the Frequency and Name fields. Leave all the other fields at their default values.
“The BC RR channels are pretty basic so you can ignore most of the columns. The RR channels are simplex, that means that they use the same frequency for transmit and receive. Most public channels are simplex. They have no carrier tone or any other funny business. So we just have to enter the frequencies and the name. Leave the rest of the settings at the default values.”
Great Article!
Fantastic!!! … I have just purchased similar radios with only a vague hope (and minimal previous experience searching “CB radios” and “fire roads”) that they could connect to logging road channels … Hearing that there is an open-source, repository-hosted, program that will not only work on linux, but seems to favor it is an absolute delight !!
!!
No complaint, but it may be appreciated by many if you could provide a *.csv (or *.chirp / whatever) file with the logging road frequencies.. Alternatively, they can be copied into a spreadsheet from https://www.fleetwooddp.com/pages/bc-logging-roads-resource-road-frequencies, and then the 2 relevant columns can be copied into a chirp-exported *.csv, and using e.g. vim, one can systematically move and number the entries.
I’m assuming I cannot program a Cobra 45wx citizens band 2-way handheld cb radio with logging road channels. Is that correct?
Your assumption is correct. CB and VHF are not the same things.
not to be a Debbie downer, but you should be aware provincial RR channels and LADD are restricted to licensed COMMERCIAL radios and individuals or organizations that hold a commercial license. the baofeng is classified as Amateur radio (HAM) , so you have a couple problems here. you have to have an Amateur radio licence to posses and use and Amateur radio, second Amateur (HAM) radios are restricted to designated frequencies. Commercial radios are easy to identify as they are non programmable (no buttons) they need to be set up by professionals. The frequencies were removed deliberately to keep the general public from spamming the frequencies with chit chat and causing a dangerous situation for those who are working , and incidentally paid for and are legally authorized to use those channels . Finally, HAM radios in particular Chinese baofeng broadcast a dirty signal that is at a much different standard than commercial radios. I’m not a cop, just beware you are you are breaking a variety of federal communication laws, the fines are well into the thousands of dollars and simply possessing the radio is a crime. I strongly encourage you to not broadcast of RR or LADD channels, as this is the fastest way to draw attention of law enforcement to your area. And i am sure you don’t want to jeopardize the safety of the guys working. The correct course of action is to purchase a licensed commercial radio and buy a licence to broadcast on RR /LADD channels, if you have a need. another option if you are just listening is to purchase a VHF scanner.
You might want to double-check the advice you’re giving out. RR and LADD are public channels. The RR channels in particular are for public safety on FSRs. How are you supposed to communicate with logging trucks if you don’t have your radio programmed for that channel?
All radios are programmable. I program my Kenwood and Icom radios at home too. There’s no difference between paying a shop or doing it yourself. The Baofengs are just more convenient since you can type in the frequencies without using a computer.
The RR and LADD frequencies are publically available. You 100% do not need a license to broadcast on those channels. What you are saying is false Chris.
According to ISED Canada website, “Two way radios using these channels [RR – British Columbia Resource Road Channels] require a mobile radio licence. The use of amateur, marine or user programmable radios is not permitted.” Here’s a link to the website: https://www.ic.gc.ca/eic/site/smt-gst.nsf/eng/sf11127.html . I suggest you contact ISED Canada for clarification.
See the recent update to this post for 2021. ISED reached out to us and explained everything.
From the government website on RR channels:
“Two way radios using these channels require a mobile radio licence. The use of amateur, marine or user programmable radios is not permitted.”
See the recent update to this post for 2021.
“The RR and LADD frequencies are publically available. You 100% do not need a license to broadcast on those channels. ”
YOU don’t need a license. Your radio does. And in order to be licensed, the radio must be a type-approved land mobile radio.
The “it’s a public channel, it’s all about safety” does not mean those channels are a free-for-all. Yes, ANYONE can use them… with the appropriately licensed hardware. Buy a land mobile radio, pay the license fee, have the radio PROPERLY programmed* for those public channels, and you’re good to go. It’s ridiculously simple, nobody has an excuse to be without.
And no, it doesn’t require $1000+. Several Lower Mainland radio shops now sell packages targeted to off-roaders, starting at around $300 for a handheld, or $400 for a mobile radio, including the antenna. One store is even now selling “compliant” (ie. factory locked) handhelds for around $100, 100% legal for land mobile use.
*I note, “PROPERLY programmed”… because anyone following the instructions posted here will not have their radio properly programmed for the RR channels. This is one of the benefits of having a professional program your radio vs. encouraging newbies to just DIY: they not only know the proper specs, they probably already have ready-to-go codeplugs for almost any radio out there, to ensure everything is up-to-snuff.
You’re making it seem like programming a radio is some magical black art. It’s actually really simple and the guys at the radio shop do the same thing as explained in this article. It’s simple and easy to do yourself.
Can you share a link for the radio shop offering “factory locked” handhelds for around $100?
There is only ONE version of the UV-5R radio which has been certified for use as a commercial band radio, and locked down against end user programming. Pay attention to the specific model number.
All other versions are “open” radios (end user programmable) and are NOT permitted to be used. Amateur radios are also locked to transmit ONLY on amateur frequencies. If they are capable of transmitting outside of these bands, they are not amateur radios. To use Commercial band channels, you must have a licence, and use certified (approved) makes and models of radios only.
See the recent update to this post for 2021.
Tell me you didn’t read the article without telling me you didn’t read it. Sad Ham…
I recently looked-up the UV-5R on Innovation, Science and Economic Development’s certified Radio Equipment List, and it appears that it is now type-certified for land mobile use on VHF and UHF frequencies. Certification number: 25962-P51UV. So it it apparently can be licensed for RR frequencies.
“…it appears that [the UV-5r] is now type-certified for land mobile use on VHF and UHF frequencies”
Not exactly. Specific variations are. To be type-certified for land mobile use, a radio must at the very least not be field-programmable… which in this case means, it must come from the factory with the keypad locked out.
There are variations that are certified as amateur radios (unable to transmit outside the amateur bands) and variations that are LMR compliant… those are the only ones that can be legally sold in Canada. Otherwise you have to have them shipped to you from somewhere else.
Recently purchased 2 uv-5r’s from a Canadian distributor and found them locked to the amateur frequencies. Is it possible to unlock them to allow for the RR amd LADD channels?
You can’t “lock” a UV-5R radio. You can always change the frequencies. This article explains how to do that.
I think there is a bit of confusion on the legality of Baofeng radios and their clones in Canada. First off, posession of any radio regardless of it’s type is not a crime. You can own it but there are regulations set out by industry canada for their use. If You want to transmit on an amature or HAM frequency You must be certified, have a call sign and only transmit using the minimum amount of power required to reach your intended contact. Baofengs are capable of broadcasting on many frequencies inside and out of the amateur bands, if You are a certified HAM operator You have a greater responsibility to not transmit out of band as well as conduct Your transmitting using proper ediquitte. Many logging outfits and other buisnesses use commercial radios that are tuned to a repeater that requires them to be “keyed up” before transmitting this is different than simplex comms on the RR frequencies. I think it is a reasonable idea to have one of these cheap radios to listen for trucks calling out mile marker locations on their way up and down the mountain but there is no way You should use the transmit key without a licence, certification or a life and death situation. Buy some 500mW FRS radios or CB if You want something that will allow You to communicate without issue or better yet take a HAM course and get certified! It’s free other than paying the examiner that gives You the test and it is a lifetime certificate. Then You can HAM it up with those Baofengs to your hears delight. CQCQCQ VA7XML
See the recent update to this post for 2021, we’ve had thorough discussions with ISED to clear things up.
“First off, posession of any radio regardless of it’s type is not a crime.”
Not entirely accurate. Here’s how it was explained to me by ISED Spectrum Management:
From the Radiocommuncations Act:
4 (1) No person shall, except under and in accordance with a radio authorization, install, operate or possess radio apparatus, other than
(a) radio apparatus exempted by or under regulations made under paragraph 6(1)(m); or
(b) radio apparatus that is capable only of the reception of broadcasting and that is not a distribution undertaking.
https://laws-lois.justice.gc.ca/eng/acts/r-2/page-1.html#h-423829
4(I)(a) covers things like CB, GMRS, RC cars, garage door openers, and all manner of other devices that are “license-exempt”.
4(I)(b) would be things like scanners, or your standard car radio.
“Radio authorization” would be such things as, say, a land mobile license applied to a given land mobile (commercial) radio.
So, 4(I) of the Act prohibits possession of a ham radio… UNLESS:
Exemption of Radio Apparatus Operated in the Amateur Radio Service
15.3 A radio apparatus that is operated in the amateur radio service at a mobile or fixed station is exempt from subsection 4(1) of the Act, in respect of a radio licence, if
(a) a person who operates the radio apparatus is an individual who is the holder of one or more of the certificates or licences referred to in section 42; and
(b) the operation of the radio apparatus in the amateur radio service is in accordance with the technical requirements referred to in section 45.
https://laws.justice.gc.ca/eng/regulations/SOR-96-484/page-2.html#h-1001735
So in short: it’s not legal to own a ham radio unless you have your ham qualification, or one of a few other specific operator’s certificates.
If you ARE a qualified ham, there’s almost no limit to what radios you can use to operate on the ham bands, including land mobile radios.
We already covered this. Yes, it is listed in the regulations but the law is not enforced and never has been.
For those who are concerned about the laws, it does sound like a good option to obtain a HAM license instead of paying yearly for the land mobile license. It would be a lot cheaper and might open some doors to a new hobby.
Incase my comment was not clear regarding the rules here is a link to the rules in BC.
https://www2.gov.bc.ca/gov/content/industry/natural-resource-use/resource-roads/radio-communications
Hello, I have been working in the bush near Port Renfrew and i have the HBO radio direct frequency but am unable to find the HBO repeater frequencies. If any one knows these and would like to share it would be much appreciated. thanks
Baofengs being illegal in Canada (Alberta specifically), or at least comething that cops care about, is TOTAL BS! I’ve never even heard or imagined that they would be!
I was doing some electrical work in a family friend’s house and noticed eight Baofengs with chargers on a basement workbench. I mentioned how much I like that particular radio and he agreed, they’re great, he uses them while driving with his other car-fanatic buddies on long road trips and at days on the racetrack.
The Border services d—–bags love to confiscate things, and mine got through no problem (Amazon.com)
Anyone have any issues getting them imported?
I’ve never had an issue getting them from Amazon.com. You have to get them from the American Amazon but there are no issues with shipping over the border.
Ordered one end of November from Amazon.ca, was here in 2 weeks. Was easy to program.
Forgot to include the point why I mentioned that family friend with the eight Baofengs: He is an RCMP Officer.
I am having a tough time getting software for my Radio. Will Chirp load up a Tad M10. No one told me you can program it not to transmit. So I have a Brand new $1000 Tad M10 receiver I bought 6yrs ago. I just bought a fairly good shape Tad m10 from a pawn shop that works as it should. So I have all the manuals but no software program. Besides maybe Chirp can’t make changes to the transmitting. Still would like to make it easier to load up frequencies on the latest Tad M10. Thanks
If I wanted only to listen to FSR traffic and logging trucks to maximize my (and their) safety, but I don’t want to transmit, what scanner/radio would you all recommend? Thanks!
The BaoFeng UV-82HP is the best radio on the market for the money. They cost about $100 CAD. You have to buy them from the American Amazon site for reasons explained in the article.
It would be silly to only listen to FSR traffic. You’re not doing yourself or your family any favours doing that. It is necessary, and required, to call out kilometer markers so other users of the road know that you’re coming. Get a Baofeng and protect yourself and your family.
So who knows how you can go about using a Icom Vhf radio but to unlock it for transmitting on RR frequency. Yes I know this is a No no but honestly I think we all would rather be safe on the roads them worry about some silly fine or license. Any support is appreciated.
All you need is the programming software and a programming cable.
Check here for the software, it depends on the your radio model: https://www.icomjapan.com/support/firmware_driver/
You should be able to get a programming cable for cheap on Amazon.
The genie is out of the bottle. It was much easier in the old days for the government to restrict what radios could be used and where. With the flood of the cheaper programmable radios it would be near impossible to put the genie back in the bottle.
The best and smart thing to do is make it easy to find information about common sense radio usage and what channels use what settings. For instance, Resource Roads are narrow band 12.5 KHz – while the LADD channels are still using the older 25 KHz wide-band.)
Set the TX so it will Time Out (TO), at a minute or less. That is the length of time the radio will transmit before stopping automatically.
I have seen where a portable had the TX button accidentally pushed down between stuff on the truck seat. Had to listen to the person’s music playing for nearly 20 min until the battery probably went dead.
And I didn’t even like their taste in music
The Midland WR400 is the best NOAA weather radio available. It is essential to receive daily weather alerts, especially for people living in severe weather areas.
The older UV-5Rs are very noisy on transmit. They produce 2nd and third harmonics which are far above the -40dB limit and are thus produce ‘harmful interference’ to communications legitimately using those bands (288 MHz, 433MHz). The new ones appear to be much cleaner and are essentially GT-5Rs.